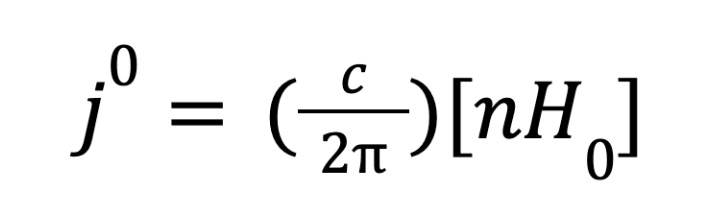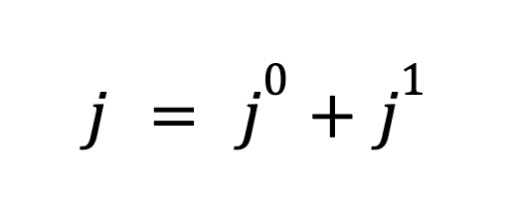When Soviet Scientists Won the Cold War: Understanding Stealth with Abbey

A brief history and introduction to Pyotr Ufimstev's foundational work on stealth technology, using Abbey.

In the early 1970s, Lockheed Martin engineer Denys Overholser discovered the key to stealth technology hidden in a stack of translated Soviet technical papers. Disregarded by the Soviet academic elite, and unheard of in the United States, Pyotr Ufimstev had worked out calculations that would help win the Cold War – but for the other side.

I’d like to provide some historical background and then work through a small part of Ufimtsev’s paper, using Abbey. You can find a course made to take you through some of the paper here, which provides general scientific background (textbook chapters), notes, quizzes, shared chats, and chat-able documents.

Historical Background

Soviet censors didn’t believe that Pyotr Ufimstev’s obscure book Method of Edge Waves in the Physical Theory of Diffraction had much use, so they permitted its publication and translation into English. But when the book arrived at Lockheed Martin’s Skunk Works division – the famed team behind the SR-71 Blackbird and the U-2 spy plane – a bright engineer quickly understood that it was exactly what he needed.

The U.S. had a problem: American-designed planes used in the Yom Kippur War proved shockingly vulnerable to Soviet radar, resulting in a devastating loss of aircraft. Military aircraft manufacturers like Lockheed Martin and Northrop Grumman tried their best to reduce their planes’ radar cross section – the measurement of how large an object would appear on radar – for years, but even the stealthiest planes, like the U-2 spy plane, still lit up Russian radar.

Ufimstev’s paper provided a superior method for calculating radar cross sections, which had previously been imprecise. An important implication of his work, which was new to many, was that an aircraft’s shape – not its size or material composition – was the most important factor in determining how large it would appear to radar systems. American designers could calculate the radar cross section of a plane’s design on computers and optimize for stealthiness.

The first plane designed using this method was the F-117 Nighthawk. Its radar cross section was orders of magnitude below anything ever designed before. In fact, at the military’s radar proving ground, where Lockheed was competing for a project, Lockheed complained that the pole on which their plane model was sitting had a larger radar cross section than the plane itself. So Lockheed developed a “stealth pole” to mount the stealth plane. When Northrop’s program manager saw the results of the tests on the new pole, he said, “If they can do that with a frigging pole, what can they do with their damned model?”

The plane would be a closely guarded secret for years, first entering major combat operations during Desert Storm. It would fly 1,300 sorties in Iraq without being downed once.

In this story, the great American advance came not from a new brilliant inspiration or new experiments, but from a close reading of the literature. I hope that Abbey can help more people read and research as effectively as the engineers at the Skunk Works.

Note: The above story is from Skunk Works: A Personal Memoir of My Years at Lockheed by Ben Rich and Leo Janos (first published in 1994). Other works tell the history of stealth differently. They may emphasize, for example, U.S. supercomputing superiority, which allowed the calculations to be performed; the improved onboard computer systems required to fly a plane whose shape was not optimized for flight; and other papers published in the United States around the early 1970s with implications for stealth (see a Northrop paper here, published in 1972, which cites other American sources).

—

The Book: Method of Edge Waves in the Physical Theory of Diffraction

Dennys Overholser called the paper “so obtuse and impenetrable that only a nerd's nerd would have waded through it all.” I’ll try and wade through some and leave the rest as an exercise to the reader.

Even if you don’t have much of a background in this subject, you might be surprised at how much you can learn by going through the course on Abbey if you’re willing to put in some effort. For comments or corrections, please reach out to gordon@us.ai.

Technical Preliminaries

Radar waves, like visible light, radio waves, or microwaves, are electromagnetic waves. These waves travel through space with a particular frequency. Radio and radar waves generally have very low frequencies, while microwaves or gamma rays have very high frequencies (visible light is in the middle). Radar seeks to detect distant objects by transmitting electromagnetic waves and then detecting those waves’ reflection off objects.

What Are Electromagnetic Waves?

Electricity and electromagnetic waves are closely related. Electric current is generated when there is a voltage potential across a wire. On the negative end of the battery there is an excess of electrons, and on the positive end there is a dearth of electrons. Electrons nearest the positive end of the wire will drift toward the positive terminal of the battery, and electrons on the negative end will drift outward.

Now to consider electromagnetic waves again: according to Ampere’s Law, an electric current generates a magnetic field around itself. An electromagnetic wave is caused by changes in the electric and magnetic fields. So a current that is changing direction a lot (like an alternating current) simultaneously changes the magnetic field around it and generates a wave spreading out from the wire (electro - magnetic). The frequency with which these electrons wiggle back and forth is the frequency of the wave. The wave propagates via photons, which carry information about this frequency.

When the wave (the photons) hits a conducting body, the electromagnetic wave induces an oscillating current – effectively the reverse of the process just described. In a material that reflects electromagnetic waves, it means that the wave strikes the body, which generates current, which then re-generates the wave (i.e., re-releases the photons). Metal reflects electromagnetic waves very well.

As a side note: You may ask, “What exactly is doing the waving, and what does the wave look like in space?” There is no good answer. Some people say that “light is both a particle (a photon) and a wave,” but this description is often unhelpful. A very good source for learning about these phenomena is Richard Feynman’s lectures on Quantum Electrodynamics.

Foreword

The foreword of the paper starts defining the scope of “the physical theory of diffraction” (the title of the work) and where it differs from prior work. It starts with reference to “geometric optics,” an old theory that describes light as rays (straight lines), and its counterpart, the “geometric theory of diffraction.” It also describes “physical optics”, which uses a more modern wave interpretation of light. This paper is its diffraction theory counterpart.

The foreword explains how it differs from the previously proposed “geometric theory of diffraction”:

In the ‘geometric theory of diffraction’ proposed by Keller, [...] the concept of diffraction rays advanced to the forefront. This concept was expressed rather as a physical hypothesis and was not suitable for representing the field in all of space: it was not usable where the formation of the diffraction field takes place (at the caustic, at the boundary of light and shadow, etc.). Here it is impossible to talk about rays, and one must use a wave interpretation. (Page v)

So the old theory of diffraction relied upon an imprecise interpretation of light as things moving in straight lines. However, this interpretation is inadequate when examining a body closely (like at the “boundary between light and shadow” – i.e., at the edge). The new theory relies on a more precise wave interpretation of light.

Do we care about this difference in accuracy? The foreword explains the use-case:

It is clear that the physical theory of diffraction is a step forward in comparison with physical optics, which in general neglects the additional (edge) currents. The results obtained in this book show that with a given wavelength the physical theory of diffraction gives a better precision than physical optics, and with a given precision the physical theory of diffraction allows one to advance into the longer wave region and, in particular, to obtain a number of results which are of interest for radar where the ratios of the dimensions of the bodies to the wavelength do not reach such large values as in optics. In addition, the physical theory of diffraction encompasses a number of interesting phenomena which are entirely foreign to physical optics. Thus, in a number of cases the additional currents give, not a small correction to the radiation field, but the main contribution to this field (see especially Chapters IV and V). (Page vi)

So while the old theories may give good-enough results for optical waves (light that you can see traveling around like a ray), this theory remedies significant errors for longer waves (i.e., radar).

What is Diffraction?

You may still be wondering what “diffraction” means (which is not defined in the paper). Diffraction occurs when a wave meets an obstacle or an opening. It is the bending of the wave around the obstacle (if it bends a lot, the object might have no “shadow”). Think of a rock in a pool of water: waves with a high wavelength will seem to pass around it, while shorter waves will leave a visible trail of still water behind the rock where the waves could not reach. You can refer to an explanatory video here.

The relevance to this paper (and to radar) – besides that “diffraction” is in the title – is that the calculations involving “diffraction currents” give the correction factors attributable to this theory. In the words of the paper, “In certain cases, one is obliged to consider the diffraction interaction of the various edges – that is, the fact that the wave created by one edge and propagated past another edge is diffracted by it (secondary diffraction).” (Page v)

Introduction

Now we enter the paper. Ufimtsev first demonstrates a physical optics approach to understanding a scattered wave (i.e., reflected, but not only straight back). The first equation is:

This equation is a bit strange even to the mathematically adroit. To explain: j is the surface current density, c is the speed of light, n is the “normal” vector, and H represents the magnetic field vector. Ufimstev will explain that j0 is the surface current density in the “uniform” part (the part not accounting for edge currents, his contribution). The normal vector is just a line that sticks out from the surface, and the notation above means that its cross product is being taken with respect to another line, the line associated with the magnetic field. The cross product simply means that the result is a current (line) flowing along the surface, whose magnitude is largest when the surface is exactly perpendicular to the wave. When the surface is slanted with respect to the magnetic field, the generated current density is lower.

(A side note: the constant on the left involving the speed of light appears as though it messes up the units, but Ufimstev is using an alternative scheme in which the speed of light has no units. If you looked up this equation elsewhere, the c/2pi constant is removed)

As promised Ufimstev then gives the equation:

…where the total surface current density is the sum of the simplistic calculation above (j0) and a more complicated calculation (j1) that matters around the edges of the surface. The simple current density is called the “uniform part” and the other one is called the “non-uniform” part.

Why do we care about surface current density again? Recall that an electromagnetic wave is “reflected” when it is absorbed by the electrons on a surface (this generates current) and then released again (that is, it emits photons). So the surface current density determines how much the wave gets reflected. Ufimstev notes, “The scattered field created by the current [see the first equation] is then found by means of Maxwell's equations.” So once we have the current, we can figure out the generated wave (this is a known procedure covered outside the paper; they are very famous equations).

Chapter 1: Diffraction by a Wedge

If you are concerned with calculating the radar cross section of a plane that looks like the F-117 Nighthawk, wedges are very important. The Nighthawk is composed almost entirely of flat surfaces at harsh angles. These are wedges.

The paper proceeds by recapitulating a rigorous calculation of the scattered wave, which was first found by Arnold Somerfeld. It then uses the “physical optics approach” to find j0, the “uniform part.” The “non-uniform” part is the difference between the two.

At this point the paper becomes mathematically serious, and I cannot go through it all here.

—

Conclusion

I hope that the work so far has given you an idea of the contribution of Soviet mathematics to U.S. stealth technology and has introduced you to some of what you can learn on Abbey. And hopefully it’s inspired some of you to learn more about electricity and magnetism; I had too much fun with this project.